描述
P1.4.5.1 慣性矩的定義
P1.4.5.2 慣性矩與物體形狀
P1.4.5.3 確認斯坦納定理
對於任何質量元素 距離旋轉軸的剛體,其轉動慣量為
I_i = \sum m_i r_i^2
對於質量為 且半徑為 的軌道上的粒子,我們可以說
I = m \cdot r^2
轉動慣量是根據試驗體安裝在其上的扭軸的振盪週期來確定的,該扭軸通過螺旋彈簧彈性地連接到支架。系統被激勵為簡諧振盪。對於已知的導向角量,可以使用振盪週期 通過以下公式計算試驗體的轉動慣量:
I = D \left( \frac{T}{2\pi} \right)^2
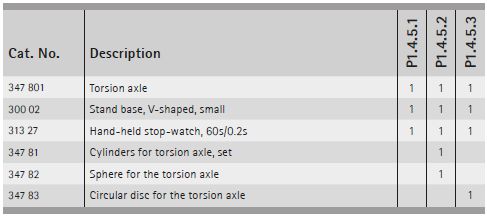
在實驗 P1.4.5.1 中,”質點”的轉動慣量被確定為距離旋轉軸的距離 的函數。在此實驗中,一根帶有兩個等質量重物的桿橫向安裝在扭軸上。兩個重物的重心距旋轉軸的距離相同,因此系統在沒有不平衡重量的情況下振盪。
實驗 P1.4.5.2 比較了空心圓柱體、實心圓柱體和實心球體的轉動慣量。此測量使用兩個質量相等但半徑不同的實心圓柱體。此外,此實驗檢查了一個質量和半徑均等於其中一個實心圓柱體的空心圓柱體,以及一個具有與其中一個實心圓柱體相同轉動慣量的實心球體。
實驗 P1.4.5.3 使用平圓盤驗證斯坦納定律。此處,測量了圓盤距旋轉軸不同距離 的轉動慣量,並與圓盤重心軸的轉動慣量 進行比較。此實驗確認了以下關係:
I_A – I_S = M \cdot a^2











商品評價
目前沒有評價。