描述
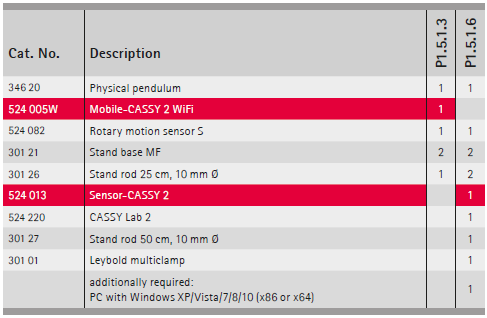
P1.5.1.3 棒形擺的振動及地球重力加速度的測定,使用旋轉運動感測器進行測量
P1.5.1.6 可變重力加速度的擺(變重力擺)
在物理擺的情況下,考慮到剛體的質量分佈。振動周期 T 的計算基於繞懸掛點的慣性矩 J、質量 m 和懸掛點距離質心的距離 s。
T = 2\pi \sqrt{\frac{J}{mgs}}
縮減擺長 lR 是具有相同振動周期的數學擺的長度。通常無法精確確定縮減擺長,因為慣性矩或質心的確定很難。在反轉擺的情況下,改變質量分佈使得兩個旋轉軸的振動周期相同。因此,縮減擺長 lR 對應於兩個旋轉軸之間的距離,因此非常精確已知。
在實驗 P1.5.1.3 中,研究了棒形擺的振動,即一種簡單的物理擺。使用旋轉運動感測器 S 記錄了擺的振動隨時間的變化。角度 a(t)、角速度 w(t) 和加速度 a(t) 被比較。此外,從測得的振動周期 T 確定了擺的有效長度。研究了周期 T 隨振幅 A 變化的依賴關係。對於小偏角,擺的振動近似為谐波振動,周期與振幅無關。對於大偏角,這個近似不再成立:振幅越大,周期越長。棒形擺被應用為可逆擺。通過調整擺的設置,在棒的兩側設置了兩個懸點。兩個滑動重物的位置影響振動周期。當擺正確調整時,它在兩側以相同的周期 T 擺動。有效擺長 lr 對應於兩個懸點之間的距離 d。根據有效擺長 lr 和周期 T 計算出重力加速度。
在實驗 P1.5.1.6 中,組裝和研究了一個可變重力加速度的擺(變重力擺)。振動平面被傾斜,從而減少了重力加速度。這導致依賴傾斜角度而有不同的振動周期。在實驗中確定了周期隨傾斜角度變化的依賴關係。此外,還模擬了不同天體上的重力加速度。








商品評價
目前沒有評價。