波動光學：繞射

描述

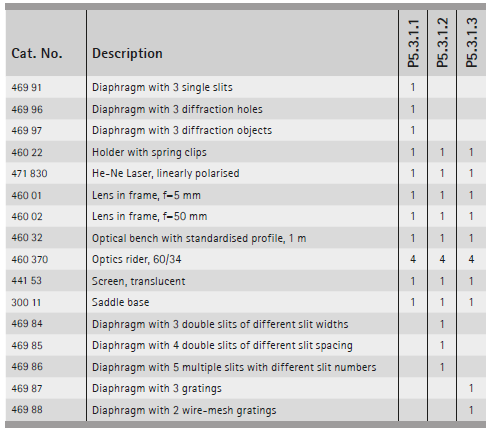
P5.3.1.1 狹縫、柱狀物和圓形光闌的繞射

P5.3.1.2 雙縫和多縫的繞射

P5.3.1.3 一維和二维光柵的繞射

 

實驗 P5.3.1.1 研究了狹縫繞射的強度最小值。對於寬度為 b 的狹縫，它們相對於光軸的角度 Jk由以下關係給出：

\(\sin \varphi_k=k \cdot \frac{\lambda}{b}(k= 1; 2; 3;…)\)

 

根據巴比涅定理，柱狀物的繞射產生類似的結果。對於半徑為 r的圓形光闌的繞射，可以觀察到同心繞射環；其強度最小值可以使用以下關係在角度 Jk 處找到：

\(\sin \varphi_k=k \cdot \frac{\lambda}{r}(k= 0.610; 1.116; 1.619;…)\)

 

實驗 P5.3.1.2 探索了雙縫繞射。來自第一個狹縫的次波與來自第二個狹縫的次波的相長干涉產生強度最大值；在狹縫中點之間的距離 d給定的情況下，這些最大值的角度 Jn 由以下公式確定：

\(\sin \varphi_k=n \cdot \frac{\lambda}{d}(n= 0; 1; 2;…)\)

 

各個最大值的強度並不是恆定的，因為單縫繞射的效果疊加在雙縫繞射上。對於多於兩個且間距相等的狹縫繞射，其干涉最大值的位置保持不變。在任意兩個最大值之間，我們還可以檢測到 N−2 個次級最大值；對於固定的狹縫寬度 b和增加的狹縫數量 N，其強度會減小。

實驗 P5.3.1.3 研究了單線光柵和交叉光柵的繞射。我們可以將交叉光柵視為兩個相互垂直排列的單線光柵。繞射最大值是直線方格矩陣圖案的“節點”處的點。