描述
P3.1.6.1 在自由空間中測定球的電容
P3.1.6.2 在金屬板前面測定球的電容
絕緣安裝在自由空間中的帶電導體相對於無限遠參考點的電勢差 與物體的電荷 成正比。我們可以用以下關係來表示:
Q=C \cdot U
並稱C為物體的電容。因此,例如,自由空間中半徑為r的球體的電容為:
C = 4 \pi \epsilon_0 r
因為帶電球體相對於無限遠參考點的電勢差為:
U = \frac{1}{4 \pi \epsilon_0} \cdot \frac{Q}{r}
\epsilon_0=8.85 \cdot 10^{-12} \frac{As}{Vm}
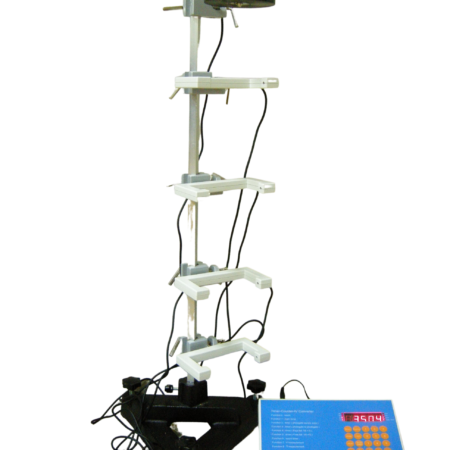
實驗 P3.1.6.1 通過給球體充上已知高電壓U並使用作為庫侖計連接的電表放大器測量其電荷 來確定自由空間中球體的電容。測量針對不同的球體半徑 進行。評估的目的是驗證比例關係。
Q \propto U
C \propto r
實驗 P3.1.6.2 顯示出物體的電容也依賴於其環境,例如與其他接地導體的距離。在此實驗中,半徑為r的球體被安排在與接地金屬板距離 處,並使用高電壓 進行充電。現在該裝置的電容為
C = 4 \pi \epsilon_0 \cdot r (1+ \frac{r}{2s})
評估的目的是確認在球體和金屬板之間任意給定距離s下,電荷
Q和電勢差U之間的比例關係。








商品評價
目前沒有評價。