描述
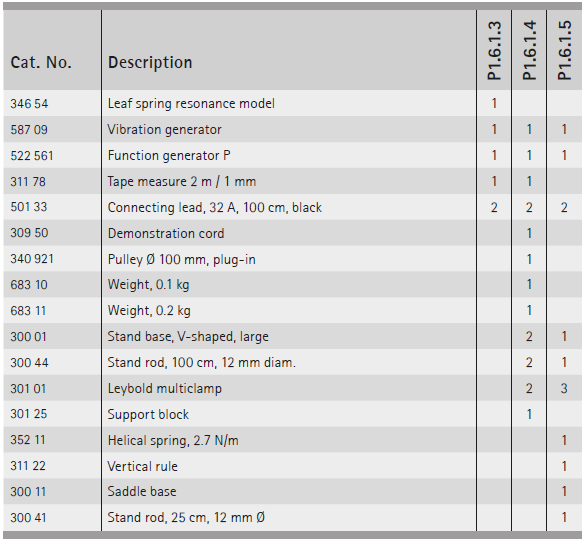
P1.6.1.3 調查葉片彈簧模型的共振振動,並確定波長
P1.6.1.4 在弦上產生站立波,並確定波長
P1.6.1.5 在螺旋彈簧上產生站立波,並確定波長
當兩個耦合的振動系統依序執行相同類型的振動時,會形成波。例如,可以在彈性繩上形成橫波,或者在螺旋彈簧上形成縱波。振動狀態的傳播速度 – 相速度 v – 與振動頻率 f 和波長 λ 之間有以下關係:
\(v = \lambda \cdot f\)
當繩子或螺旋彈簧兩端固定時,會在端點處產生反射,導致“出射”和反射波的重疊。根據繩長 s 的不同,某些特定頻率下這些波的重疊形成靜態振動模式 – 站立波。站立波中兩個振動節點或兩個反節點之間的距離等於半個波長。固定端對應於振動節點。
\(s = n \cdot \frac{\lambda}{2}\)
\(f =n \cdot \frac{v}{2s}\)
在實驗P1.6.1.3中,使用不同的頻率 f 刺激葉片彈簧模型,並尋找共振現象。因此,振動的波長 λ 可以被確定。
\(\lambda = \frac{c}{f}\)
其中 c 為傳播速度。
在實驗P1.6.1.4中,生成橫波。通過上下移動繩子的一端並固定另一端,可以創建波。波會在固定端反射並返回繩子。對於特定的頻率,某些點保持固定(節點),而其他點則以高振幅擺動(反節點)。
在實驗P1.6.1.5中,觀察螺旋彈簧上的縱波。通過上下移動彈簧的一端並固定另一端,將波反射並返回。同樣地,對於特定的頻率,彈簧的某些點保持靜止,而其他點則擺動。





商品評價
目前沒有評價。